A qualidade é parte integrante de todos os produtos e serviços. No entanto, a conscientização de sua importância e a introdução de métodos formais para o controle e melhoria da qualidade teve seu boom somente a partir do início do século XX, e principalmente após a década de 50.
Para Moretti (2003), a competitividade, em um contexto globalizado, é a capacidade de uma organização em oferecer ao mercado mundial, alternativas capazes de motivar o consumidor a trocar produtos similares de uma organização por outra. De acordo com Agostinho (2001), a competitividade pode ser caracterizada por alguns fatores dominantes, que se modificam ao longo das décadas: custo na década de 50/60, qualidade em 70, flexibilidade em 80, tempo de resposta em 90 e, finalmente, agilidade a partir de 00.
À medida que um novo fator é estabelecido, ele deve ser rapidamente incorporado às organizações, visto que o fator anterior perde sua função de ganhador de pedido, passando a ser um qualificador de pedidos. Neste contexto, cabe às empresas a árdua tarefa de se adaptar ao mercado, reduzindo custos, melhorando a qualidade, aumentando sua produtividade, diversificando seus produtos e reduzindo lead times. Desta maneira a empresa garantirá sua sobrevivência no longo prazo, face um cenário de intensa competição.
Neste artigo, a atenção será voltada para o fator competitivo qualidade que, entre outros, impacta diretamente nos custos e na imagem da empresa. Moretti (2003) cita que a qualidade deve fazer parte do organismo vivo da organização e que a atitude de qualidade não deve ser vinculada somente a produtos físicos tangíveis, mas também a serviços intangíveis que acompanham ou podem acompanhar o produto físico.
Este autor diz ainda que, atualmente, a qualidade é um conceito incorporado ao dia-a-dia das empresas, tornando-se pré-requisito para qualquer melhoria competitiva. De acordo com Agostinho (2001), a maior qualidade possível é o preço que uma empresa de manufatura deve pagar para manter-se no mundo dos negócios. Para que isso seja obtido, é necessário que as empresas adotem a visão mais geral possível de qualidade (Moretti, 2003), visando garantir vantagem competitiva em relação ao seu concorrente.
Gráficos de Controle
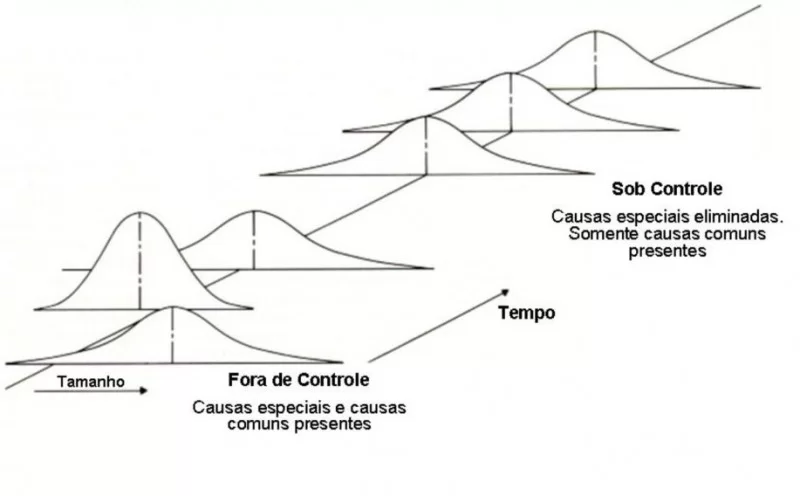
Shewhart, trabalhando no Bell Laboratories na década de 20, percebeu que a variabilidade em um processo poderia ser provocada por causas normais – aquelas inerentes e inevitáveis a qualquer processo – e por causas especiais – aquelas que são externas ao processo, resultando em perda do controle e instabilidade.
Shewhart percebeu ainda que uma intervenção em um determinado processo, baseada em uma única medida do produto, não era suficiente para garantir um processo estável e capaz de produzir dentro das especificações, e que, em contrapartida, demasiadas intervenções no processo, sem uma base estatística sólida que comprove a necessidade da intervenção (ou simplesmente tampering, em inglês) podem, ao contrário do que nosso instinto leva à pensar, resultar em aumento da variabilidade do processo, tornando-o instável e incapaz.
Sentiu-se a necessidade, portanto, de se construir uma ferramenta que fosse capaz de fornecer ao operador uma maneira simples de diferenciar causas normais de causas especiais, garantindo a qualidade do produto através de um processo estável. Shewhart criou, então, os Gráficos de Controle, que consistem em uma representação gráfica do comportamento, ao longo do tempo, de uma característica controlada (Figura 1).
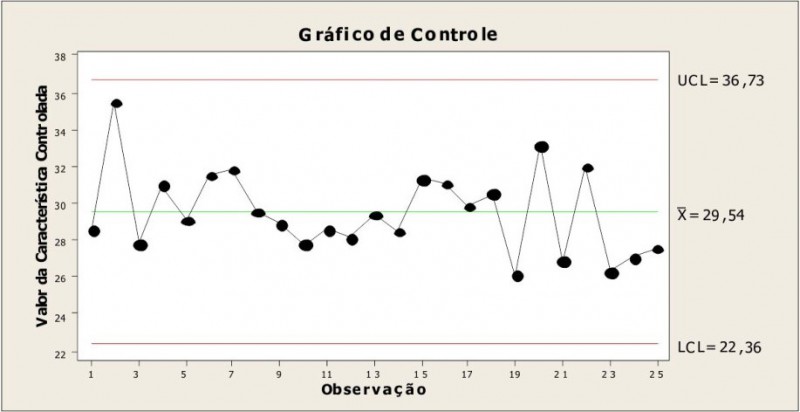
Os gráficos de controle contêm uma linha média (LM), que representa o valor médio da característica que está sendo controlada, uma linha superior de controle (LSC) e uma linha inferior de controle (LIC). Os limites de controle (LSC e LIC) são escolhidos de modo que somente variações dadas às causas normais permanecerão dentro dos limites. Basicamente, qualquer ponto que fique acima do LSC ou abaixo do LIC representará uma causa especial, a qual deverá ser investigada e eliminada.
Escolha dos Limites de Controle
Ao se trabalhar com gráficos de controle, a escolha dos limites é uma decisão crítica. Segundo Montgomery (2004), caso os limites de controle sejam muito apertados, causas normais poderão ser identificadas como causas especiais, já que a probabilidade de um ponto cair fora dos limites de controle aumenta (este é o chamado Erro Tipo I).
Inversamente, se os limites de controle forem muito abertos, pontos provocados por causas especiais podem cair dentro dos limites de controle, sendo identificados como causas normais (Erro Tipo II). Costumeiramente, adotam-se limites de controle a 3-sigmas (3 desvios padrões da média), pelo fato de gerarem bons resultados práticos (Montgomery 2004).
É de vital importância para a empresa que está aplicando o Controle Estatístico de Processo (CEP), que ela saiba distinguir causas especiais de causas normais e que, tanto erros do tipo I quanto do tipo II, sejam sempre evitados. Isto impede a ocorrência de despesas inúteis, gastos de tempo desnecessários e, principalmente, desperdício de capital humano e descontentamento dos colaboradores, gerado pela busca inútil de uma falsa causa especial.
Embora haja um consenso mundial sobre a utilização dos limites de controle a 3-sigma, há situações onde alterar tais limites pode ser muito interessante. Montgomery (2004) diz, por exemplo, que no caso onde determinadas causas especiais cujo custo de investigação ou eliminação é elevado, é mais conveniente aplicar limites de controle mais amplos que 3-sigma – talvez tão amplos quanto 3,5-sigma. Ele diz também que se causas especiais de um processo podem ser fácil e rapidamente eliminadas, com custos de investigação e de ação reduzidos, então limites mais estreitos, talvez 2,5-sigma, podem ser mais interessantes.
Na visão dos autores, esta mudança nos limites de controle também pode ser interessante quando algum processo encontra-se totalmente fora de controle e, ao mesmo tempo, não é integralmente dominado pelos colaboradores da empresa. Neste caso, é interessante usar limites de controle mais abertos, principalmente no início do programa CEP, dando aos colaboradores o tempo necessário para que as causas especiais mais graves sejam investigadas, sem que haja um desespero generalizado por não se conseguir controlar o processo. Espera-se, ao longo do tempo, que o processo seja mais bem compreendido e controlado, momento no qual serão utilizados os limites de controle a 3-sigma.
Os autores consideram ainda que, em alguns casos, limites de controle mais abertos se justificam quando coexistam causas especiais com custo muito elevados para sua eliminação e níveis de qualidade elevados (Cp e Cpk elevados – ver Capabilidade do Processo). Neste caso, é mais vantajoso conhecer a causa especial, mantendo-a sob vigilância e enxergando-a como uma causa normal no gráfico de controle. Evita-se assim, investimentos com retornos aquém dos esperados.
Capabilidade do Processo
O conceito de Capabilidade (ou Capacidade) de um Processo exprime o quanto um processo é capaz de atender às especificações do produto, através da comparação da voz do cliente (limites de especificação) com a voz do processo (limites de controle 3-sigma). A Capacidade de um processo deve fornecer um valor que permita analisar o quão adequado é o processo no momento de fabricar um produto dentro de suas especificações.
Existem diversas maneiras de analisar a capabilidade de um processo, mas sem dúvida, a melhor e mais simples delas é através da Razão da Capacidade de um Processo (RCP) (Montgomery, 2004). Existem duas formas de calcular a RCP: a primeira delas consiste no cálculo do Cp, o qual compara a variabilidade do processo com os limites de especificação; e o segundo é o Cpk, que além de comparar variabilidade do processo com os limites de especificação do produto, leva em consideração a descentralização do processo.
Montgomery (2004) diz que o valor mínimo aceitável para Cp e Cpk é de 1, ou seja, a faixa de especificação é igual a 6 desvios padrões do processo. Neste caso, o processo é capaz de produzir 99,73% de itens conformes. Entretanto, é comum buscar valores de 1,33 para Cp e Cpk, o que garante 99,9937% de itens conformes. Diz-se que este é um valor mínimo desejado. Nota-se que níveis de qualidade six-sigma implicam em valores de Cpk iguais a 2,00.
Conclusões
O Controle Estatístico de Processo é uma ferramenta que visa melhoria da qualidade dos produtos através da redução da variabilidade dos processos. Para isso, a utilização de conceitos e ferramentas estatísticas na identificação de oportunidades de melhoria e na resolução de problemas é essencial. Elas devem ser conhecidas por todos da empresa e constantemente utilizadas.
Finalmente, durante nossa vivência prática de implantação de CEP em diversos setores da indústria, observamos que o CEP vai muito além do simples controle estatístico. Na realidade, o CEP, desde que apoiado e constantemente incentivado pela alta gerência da empresa, proporciona profundas mudanças culturais benéficas para a saúde e para a longevidade da empresa.
Gostou? Nos siga nas redes sociais (LinkedIn, Facebook e Instagram) para acompanhar outros artigos e os principais resultados obtidos com a ajuda da Nortegubisian!
